Sequential Computation

Turing machines model one computational action, at
one location, per time step.

Multi-tape Turing machines model a finite number of
computations per step, either at multiple locations or
with moving tapes.

These can do some computations in quadratically less
steps than an equivalent standard Turing machine,

but they still compute with one centralized transition
function, and constant time computation involving
indefinitely far sites is physically unrealistic.

Parallel Computation

Interaction nets were developed by Yves Lafont in 1990,
as a practical model for parallel programming.

In this model, information is represented with a
collection of cells and ports, connected by wires.

During one computational step, if a pair of cells matches
a rule, they are replaced in a way that doesn’t leave
disconnected wires.

Many replacements can occur in parallel and can be
repeated until there are no rule matches (in the case of
a terminating computation).

Figure 1.  An interaction net.

Interaction Nets

Definition 1.  An interaction net is a finite set of
labeled cells (each having some number of ports), a
set of free ports not associated with any cells, and a
set of wires, connecting each port to another one.

Cells have one principal port and $n \geq 0$ auxiliary ports
(numbered in clockwise order), where $n$ is the arity of
the cell’s symbol.

Wires may connect ports of the same cell or exist as a
cyclic wire not connecting any ports.

Figure 1.  An interaction net.

Interaction Rules

Definition 2.  An interaction rule is a pair of interaction
nets having the same set of free ports.

The left-side net must consist of two cells with a wire
between their principal ports, and a wire between
each free port and an auxiliary port.

Rules may have more than two cells on the right,
allowing for an exponentially increasing number of
computations per step.

Figure 2.  Two interaction rules.
The first represents inferring $y = x$ from
$y = 0 + x$.

Reductions

Definition 3.  A reduction (step) replaces a cell pair
matching the left side of a rule with the right-side net.
After identifying an active cell pair, all auxiliary ports are
temporarily treated as being wired to corresponding
free ports.

Assume that we only use rule sets that can be applied
unambiguously – at most one rule per unordered pair
of cell symbols, and with order being irrelevant for pairs
with the same symbol.

An unambiguous rule set is called an interaction system.

Figure 3.  Two reduction steps applied in parallel.

Reductions

hoc logo { x: 450, y: 260, w: 700, h: 400 }

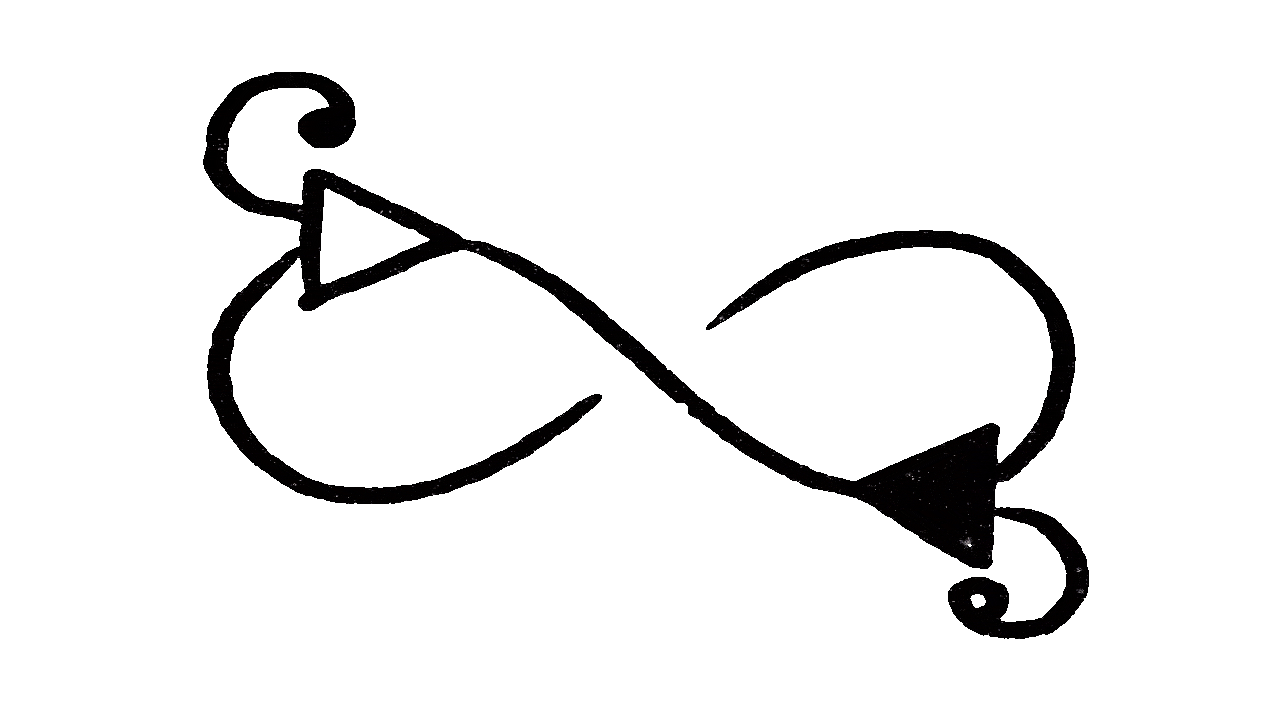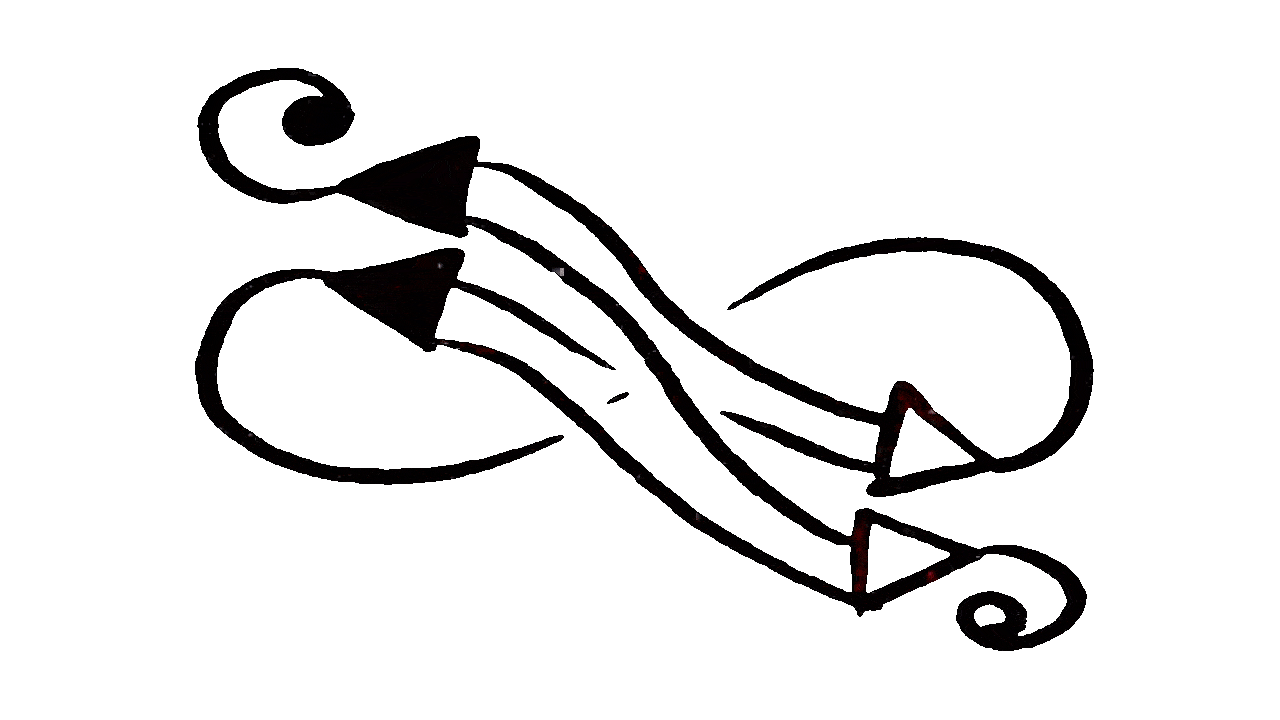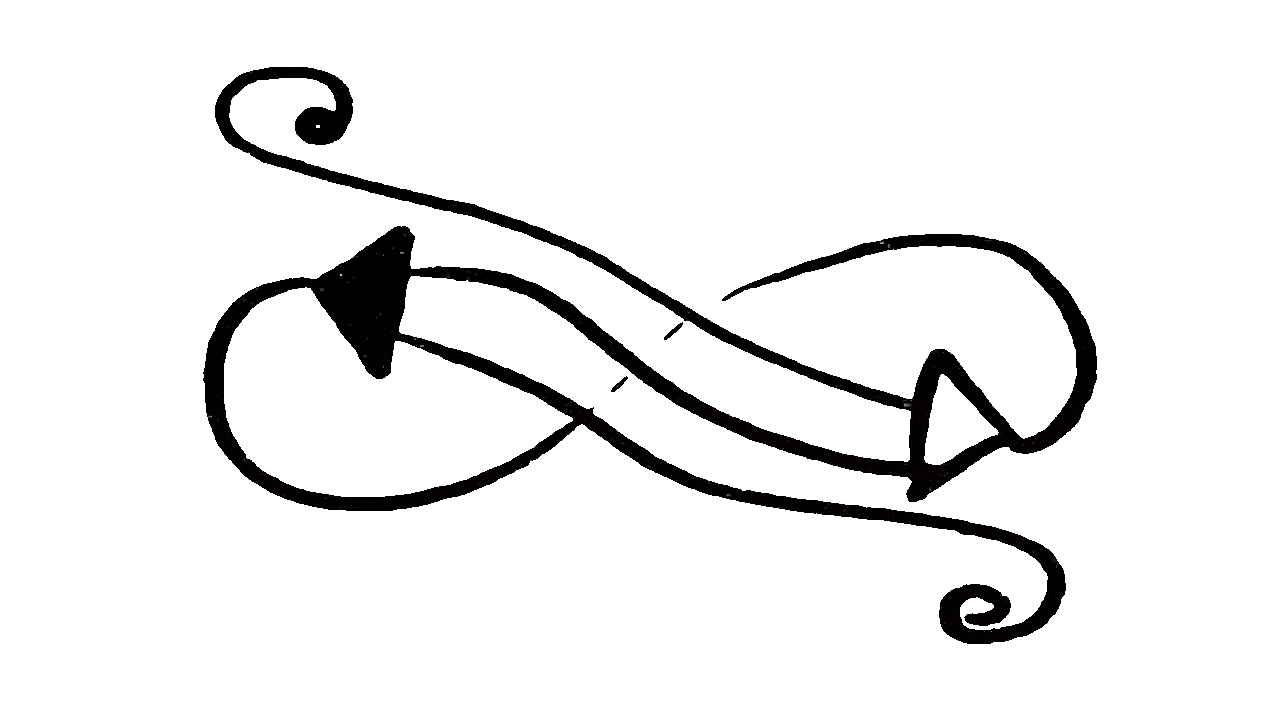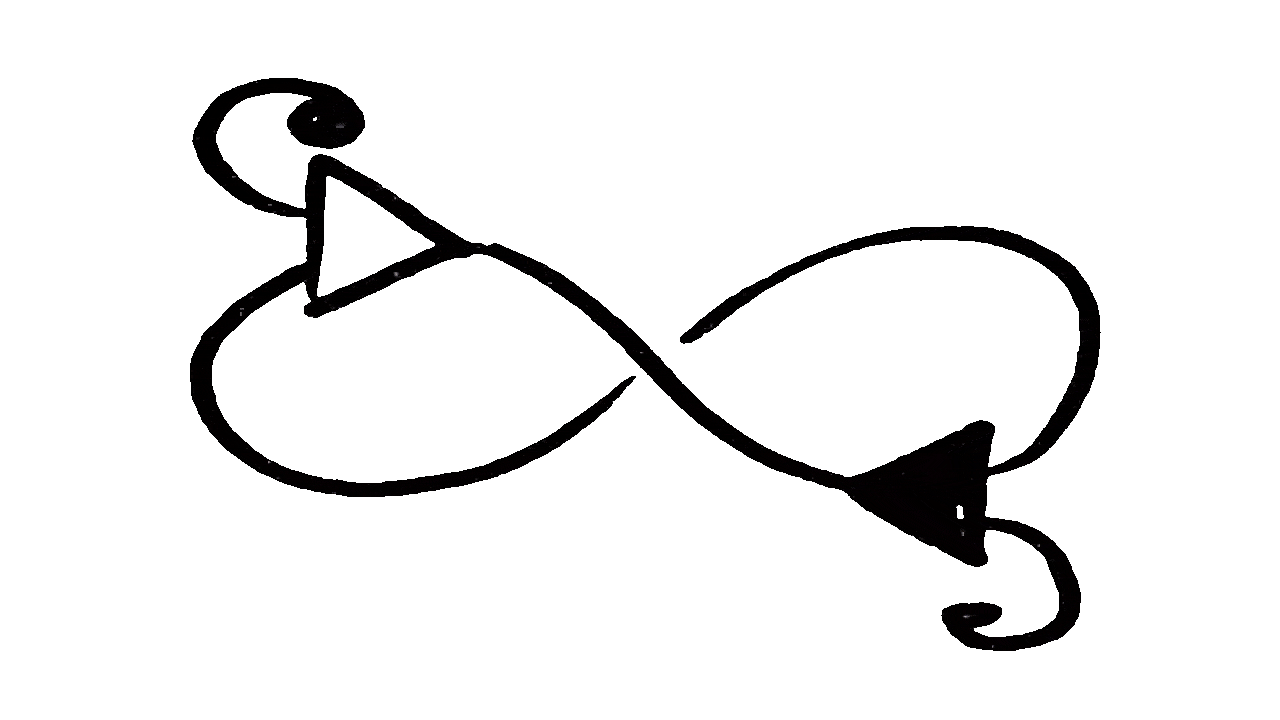
Figure 4.  An infinite reduction sequence.
            Source: higherorderco.com

Confluence

Theorem 1. (strong confluence)  If an interaction net $\tb{N}$
reduces to either $\tr{P}$ or $\tg{Q}$ in one step, with $\tr{P} \neq \tg{Q}$, then $\tr{P}$
and $\tg{Q}$ can both reduce in one step to a common net $\tm{R}$.

Proof.  Let $\{\tr{c_1}, \tr{c_2}\}$ be the cells involved in reduction of $\tb{N}$
to $\tr{P}$, and let $\{\tg{c_3}, \tg{c_4}\}$ be the same for $\tg{Q}$.

Since reductions apply only to cell pairs connected by their
principal ports, and $\tr{P} \neq \tg{Q}$, then $\{\tr{c_1}, \tr{c_2}\} \cap \{\tg{c_3}, \tg{c_4}\} = \varnothing$.

Therefore, $\{\tg{c_3}, \tg{c_4}\}$ would remain reducible after reducing
$\{\tr{c_1}, \tr{c_2}\}$ and vice versa, so $\tm{R}$ is the net with both
reductions applied.								   $\blacksquare$

Confluence

“Strong confluence” commonly refers only to the property
that branching reduction sequences can always result in
the same element.

It guarantees that two diverging and terminating reduction
sequences have the same result.

The version here with single step reductions additionally
guarantees that both sequences have the same length.
This is sometimes referred to as the diamond property.

Expression Evaluation

Example 1.  Unary addition.

Cells $0$, $s$ (successor), and $+$, along with two
interaction rules can be used reduce an addition
expression to a normal form.

From the diamond property, all possible
reductions to an irreducible form reach the same
form, with the same number of reduction steps.

In this example, an irreducible form is reached in
$4$ steps, with both rules being applied twice,
possibly in only $2$ parallel reduction passes.

Expression Evaluation

Turing Completeness

Example 2.  Implementation of Turing machines.

A Turing machine is formally specified with the $7$-tuple
$M = (\tr{Q}, \tb{\Gamma}, \tb{b}, \tb{\Sigma}, \tg{\delta}, \tr{q_0}, \tr{F})$, where:


$\tr{Q}$ is a set of states the machine can be in,
$\tb{\Gamma}$ is a set of symbols that can be stored on a tape,
$\tb{b} \in \tb{\Gamma}$ is the blank symbol (default if not specified),
$\tb{\Sigma} \subseteq \tb{\Gamma} \setminus \{\tb{b}\}$ is a set of valid input tape symbols,
$\tb{\delta} : (\tr{Q} \setminus \tr{F}) \times \tb{\Gamma} \rightarrow \tr{Q} \times \tb{\Gamma} \times \{\tg{L}, \tg{R}\}$ is a transition function,
$\tr{q_0} \in \tr{Q}$ is the initial state of the machine,
and $\tr{F} \subseteq \tr{Q}$ is a set of final states.

Figure 6.  Initial and subsequent
configurations.

Turing Completeness

Example 2 (cont’d).  Implementation of Turing machines.

The primary elements are $\tr{Q}$ (states), $\tb{\Gamma}$ (symbols), and $\tg{\delta}$
(transition function). The rest are subsets or elements of
these that denote valid initial and final conditions.

Let $\tb{...}, \tb{a}_{\tg{-2}}, \tb{a}_{\tg{-1}}, \tb{a}_{\tg{0}}, \tb{a}_{\tg{1}}, \tb{a}_{\tg{2}}, \tb{...}$ denote the sequence of tape
symbols. The read/write head starts at position $\tg{0}$ and in
state $\tr{q_0}$.

If $\tg{\delta}(\tr{q}, \tb{a}) = (\tr{q'}, \tb{a'}, \tg{L})$, with $(\tr{q_0}, \tb{a}_{\tg{0}}) = (\tr{q}, \tb{a})$, then in the
next configuration, we have $\tb{a}_{\tg{0}} = \tb{a'}$ with the head at
position $\tg{-1}$ and in state $\tr{q'}$.

Figure 6.  Initial and subsequent
configurations.

Turing Completeness

Example 2 (cont’d).  Implementation of Turing machines.

We can represent this configuration and transition with
the nets in Figure 7.

We orient the initial cells, and define interaction rules, so
that there is exactly one active pair at each step.

Figure 7.  An interaction net
simulating the same behavior.

Turing Completeness

Example 2 (cont’d).  Implementation of Turing machines.

If we instead initialize with $\tb{a}_{\tg{0}}$ and $\tb{a}_{\tg{1}}$ connected, the
equivalent rule for $\tg{\delta}(\tr{q}, \tb{a}) = (\tr{q'}, \tb{a'}, \tg{L})$ is different – with
$\tr{q}$ changing $\tb{a}_{\tg{0}}$ and turning around instead of passing
through.

Since the rule depends on the last direction, we double
the size of $\tr{Q}$, so that a state $\tr{q}$ is represented with either
$\tr{q}_{\tg{L}}$ or $\tr{q}_{\tg{R}}$ depending on the previous transition (or init).

We can then match an appropriate interaction rule and
include direction info in the next state ($\color{ff0000} q_{\tg{L}}'$).

Figure 8.  The same transition,
but with $\tr{q_0} \rightarrow \tr{q}_{\tg{R}}$ instead of $\tr{q}_{\tg{L}}$.

Turing Completeness

Example 2 (cont’d).  Implementation of Turing machines.

Since interaction nets are finite, both ends are terminated
with cells that simulate interaction with a blank symbol
and extend the tape.

Figure 9.  A tape extending reduction,
with $\tg{\delta}(\tr{q}, \tb{b}) = (\tr{q'}, \tb{a'}, \tg{R})$.

Cellular Automata

Typically, a cellular automaton (CA) is a regular network
(line/grid/etc.) of cells with discrete states.

Cells update simultaneously as a function of neighboring cells.
Each cell replaces its state with $\tg{f}(\tb{s}_{\tr{1}}, \tb{s}_{\tr{2}}, \tb{...}) \in \tb{S}$, where $\tb{s}_{\tr{i}}$ are
states of the cells in its neighborhood.

A configuration describes the state of all cells at some point in
time. It is considered to extend infinitely in all directions, and
can be represented as a function $\tm{c} : \tr{\mathbb{Z}}^{\tp{d}} \rightarrow \tb{S}$.

Figure 10.  Examples of one step of
computation, for $\tp{1}$-dimensional and
$\tp{2}$-dimensional automatons.

Finitely Specifiable Configurations

Finite configurations consist of a finite number of cells
not in some state $\tb{s} \in \tb{S}$, with all other cells being in
state $\tb{s}$.

A configuration is periodic if it’s $\tr{\ora{r}}$-periodic for at least
one vector $\tr{\ora{r}} \in \tr{\mathbb{Z}}^{\tp{d}}$, meaning the state of any cell $\tr{\ora{n}}$ is
the same as cell $\tr{\ora{n}} + \tr{\ora{r}}$.

A $\tp{d}$-dimensional configuration is totally periodic if it’s
$\red{\ora{r_{\tp{i}}}}$-periodic for $\tp{d}$ linearly independent vectors $\red{\ora{r_{\tp{i}}}}$. For
these, the configuration can be fully described by some
finite region of cells.

Finite if all other cells are in state $\tb{0}$.

Periodic if the pattern repeats infinitely.

Totally periodic if it's periodic along
two vectors that form a basis for $\tr{\mathbb{Z}}^{\tp{2}}$.

Cellular Automata

Example 3.  Implementation of $\tp{1}$-dimensional CA.

We can implement a CA computation step with two
parallel reductions. Cells interact with their left then
right neighbor, or vice versa.

Since orientation is important here, we create a left and
right-facing version of each state.

We also add left and right-facing versions of each pair of
original states (such as $\tb{\overline{rs}}$), so reductions in the second
pass can consider both neighbors.

Figure 12.  CA implementation with
and interaction net.

Symbols $\tb{p}, \tb{q}, \tb{r}, \tb{s}, \tb{t}, \tb{u}$ represent (not
necessarily distinct) states of the CA.

Cellular Automata

Figure 13.  A more concrete example with visualized labels.

Cellular Automata

Example 3 (cont’d).  Implementation of 1D CA.

If we have a finite configuration (uniform state $\tb{p}$ past
some first and last cell), we can use a similar technique
as before to allow the finite net to expand indefinitely.

We can represent periodic configurations by attaching
both ends together, if the period is even.

Figure 14.  A configuration-expanding parallel
reduction sequence, with $\tg{f}(\tb{p}, \tb{p}, \tb{p}) = \tb{p'}$.

If $\tg{f}(\tb{p}, \tb{p}, \tb{r}) = \tb{p}$, then it does not need to expand.
If also $\tg{f}(\tb{p}, \tb{r}, \tb{s}) = \tb{p}$, we can contract the net instead.

Cellular Automata

Figure 15.  Contracting on the left (since $\tg{f}(\tb{p}, \tb{p}, \tb{r}) = \tg{f}(\tb{p}, \tb{r}, \tb{s}) = \tb{p}$),
and expanding on the right.

References

1.  Lafont, Y. Interaction Nets. In Proceedings of the 17th ACM SIGPLAN-SIGACT Symposium on
Principles of Programming Languages (1989) 95-108.

2.  Lafont, Y. Interaction Combinators. Information and Computation, 137 no. 1 (1997), 69-101.